A. Pengertian Teorema Bayes
Dalam teori probabilitas dan statistika, teorema Bayes adalah sebuah teorema dengan dua penafsiran berbeda. Dalam penafsiran Bayes, teorema ini menyatakan seberapa jauh derajat kepercayaan subjektif harus berubah secara rasional ketika ada petunjuk baru. Dalam penafsiran frekuentis teorema ini menjelaskan representasi invers probabilitas dua kejadian. Teorema ini merupakan dasar dari statistika Bayes dan memiliki penerapan dalam sains, rekayasa, ilmu ekonomi (terutama ilmu ekonomi mikro), teori permainan, kedokteran dan hukum. Penerapan teorema Bayes untuk memperbarui kepercayaan dinamakan inferens Bayes.
Misalkan kawan Anda bercerita dia bercakap-cakap akrab dengan seseorang lain di atas kereta api. Tanpa informasi tambahan, peluang dia bercakap-cakap dengan perempuan adalah 50%. Sekarang misalkan kawan Anda menyebut bahwa orang lain di atas kereta api itu berambut panjang. Dari keterangan baru ini tampaknya lebih bolehjadi kawan Anda bercakap-cakap dengan perempuan, karena orang berambut panjang biasanya wanita. Teorema Bayes dapat digunakan untuk menghitung besarnya peluang bahwa kawan Anda berbicara dengan seorang wanita, bila diketahui berapa peluang seorang wanita berambut panjang.
Misalkan:
· W adalah kejadian percakapan dilakukan dengan seorang wanita.
· L adalah kejadian percakapan dilakukan dengan seorang berambut panjang
· M adalah kejadian percakapan dilakukan dengan seorang pria
P(W) = 0,5
Misalkan juga bahwa diketahui 75 persen wanita berambut panjang. Ini berarti bila kita mengetahui bahwa seseorang adalah wanita, peluangnya berambut panjang adalah 0,75. Kita melambangkannya sebagai:
P(L|W) = 0,75
Sebagai keterangan tambahan kita juga mengetahui bahwa peluang seorang pria berambut panjang adalah 0,3. Dengan kata lain:
P(L|M) = 0,3
Di sini kita mengasumsikan bahwa seseorang itu adalah pria atau wanita, atau P(M) = 1 - P(W) = 0,5. Dengan kata lain M adalah kejadian komplemen dari W.
Tujuan kita adalah menghitung peluang seseorang itu adalah wanita bila diketahui dia berambut panjang, atau dalam notasi yang kita gunakan, P(W|L).
B. Teorema Bayes
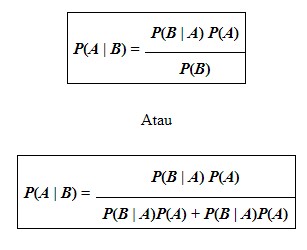
Teorema Bayes, diambil dari nama Rev. Thomas Bayes, menggambarkan hubungan antara peluang bersyarat dari dua kejadian A dan B sebagai berikut:
C. Contoh Aplikasi Dari Teorema Bayes
Di sebuah negara, diketahui bahwa 2% dari penduduknya menderita sebuah penyakit langka. 97% dari hasil tes klinik adalah positif bahwa seseorang menderita penyakit itu. Ketika seseorang yang tidak menderita penyakit itu dites dengan tes yang sama, 9% dari hasil tes memberikan hasil positif yang salah.
Jika sembarang orang dari negara itu mengambil test dan mendapat hasil positif, berapakah peluang bahwa dia benar-benar menderita penyakit langka itu?
Secara sepintas, nampaknya bahwa ada peluang yang besar bahwa orang itu memang benar-benar menderita penyakit langka itu. Karena kita tahu bahwa hasil test klinik yang cukup akurat (97%). Tetapi apakah benar demikian? Marilah kita lihat perhitungan matematikanya.
Marilah kita lambangkan informasi di atas sebagai berikut:
· B = Kejadian tes memberikan hasil positif.
· B1 = Kejadian tes memberikan hasil negative.
· A = Kejadian seseorang menderita penyakit langka itu.
· A1 = Kejadian seseorang tidak menderita penyakit langkat itu.
Kita ketahui juga peluang dari kejadian-kejadian berikut:
· P (A) = 2%
· P (A1) = 98%
· P (B | A1) = 97%
· P (B | A) = 9%
Dengan menggunakan rumus untuk peluang bersyarat, dapat kita simpulkan peluang dari kejadian-kejadian yang mungkin terjadi dalam tabel di bawah ini:
Misalnya seseorang menjalani tes klinik tersebut dan mendapatkan hasil positif, berapakah peluang bahwa ia benar-benar menderita penyakit langka tersebut?
Dengan kata lain, kita mencoba untuk mencari peluang dari A, dimana B atau P (A | B).
Dari tabel di atas, dapat kita lihat bahwa P (A | B) adalah peluang dari positif yang benar dibagi dengan peluang positif (benar maupun salah), yaitu 0,0194 / (0,0194 + 0,0882) = 0,1803.
Kita dapat juga mendapatkan hasil yang sama dengan menggunakan rumus teorema Bayes di atas:
Hasil perhitungan ini sangat berbeda dengan intuisi kita di atas. Peluang bahwa orang yang mendapat hasil tes positif itu benar-benar menderita penyakit langka tidak sebesar yang kita bayangkan. Cuma ada sekitar 18% kemungkinan bahwa dia benar-benar menderita penyakit itu.
Mengapakah demikian?
Ketika mengira-ngira peluangnya, seringkali kita lupa bahwa dari seluruh populasi negara itu, hanya 2% yang benar-benar menderita penyakit langka itu. Jadi, walaupun hasil tes adalah positif, peluang bahwa seseorang menderita penyakit langka itu tidaklah sebesar yang kita bayangkan.
Kita bisa juga meninjau situasi di atas sebagai berikut. Misalnya populasi negara tersebut adalah 1000 orang. Hanya 20 orang yang menderita penyakit langka itu (2%). 19 orang dari antaranya akan mendapat hasil tes yang positif (97% hasil positif yang benar). Dari 980 orang yang tidak menderita penyakit itu, sekitar 88 orang juga akan mendapat hasil tes positif (9% hasil positif yang salah).
Jadi, 1000 orang di negara itu dapat kita kelompokkan sebagai berikut:
· 19 orang mendapat hasil tes positif yang benar
· 1 orang mendapat hasil tes negatif yang salah
· 88 orang mendapat hasil tes positif yang salah
· 892 orang mendapat hasil tes negatif yang benar
Bisa kita lihat dari informasi di atas, bahwa ada (88 + 19) = 107 orang yang akan mendapatkan hasil tes positif (tidak perduli bahwa dia benar-benar menderita penyakit langka itu atau tidak). Dari 107 orang ini, berapakah yang benar-benar menderita penyakit? Hanya 19 orang dari 107, atau sekitar 18%.
DAFTAR PUSTAKA
M.B.A,Riduan.2006.Dasar-dasar Statistik.Bandung:ALFABETA
Pratiknya.Dasar-dasar Metodologi Penelitian dan Kesehatan, Jakarta, Raja Grapindo Persada; 2000.
Arjatmo Tjokro. Metodologi Penelitian Bidang Kedokteran, Jakarta, FKUI.
Sokidjo Notoatmojo, 1993, Metodologi Penelitian Kesehatan, Jakarta, Rineka Cipta. 1999.
Hidayat AA. Metode Penelitian Kebidanan Teknik Analisis Data. Jakarta.Salemba medika; 2007,
Riduwan. Metode dan Teknik Menyusun Tesis. Bandung. Alfabeta;2004.
https://www.idomaths.com/id/peluang5.php
http://bagaswhy.blogspot.com/2016/11/peluang-bersyarat-dan-teorema-bayes.html


Komentar
Posting Komentar