BINOMIAL
Dalam teori probablilitas dan statistika, distribusi binomial adalah distribusi probabilitas diskret jumlah keberhasilan dalam npercobaan ya/tidak (berhasil/gagal) yang saling bebas, dimana setiap hasil percobaan memiliki probabilitas p. Eksperimen berhasil/gagal juga disebut percobaan bernoulli. Ketika n = 1, distribusi binomial adalah percobaan bernoulli. Distribusi binomial merupakan dasar dari uji binojmial dalam uji signifikansi statistik.
Distribusi ini seringkali digunakan untuk memodelkan jumlah keberhasilan pada jumlah sampel n dari jumlah populasi N. Apabila sampel tidak saling bebas (yakni pengambilan sampel tanpa pengembalian), distribusi yang dihasilkan adalah distribusi geometrik, bukan binomial. Semakin besar N daripada n, distribusi binomial merupakan pendekatan yang baik dan banyak digunakan.
Percobaan binomial merupakan suatu percobaan yang memenuhi empat syarat berikut:
- Terdapat n kali percobaan.
- Masing-masing percobaan hanya dapat menghasilkan dua kemungkinan, atau hasil yang diperoleh dapat disederhanakan menjadi dua kemungkinan. Hasil yang diperoleh tersebut dapat dianggap sebagai hasil yang sukses atau gagal.
- Hasil dari masing-masing percobaan haruslah saling bebas.
- Peluang untuk sukses harus sama untuk setiap percobaan.
Suatu percobaan binomial dan hasilnya memberikan distribusi peluang khusus yang disebut sebagai distribusi binomial.
Hasil-hasil percobaan binomial dan peluang yang bersesuaian dari hasil tersebut dinamakan distribusi binomial.
Dalam percobaan binomial, hasil-hasilnya seringkali diklasifikasikan sebagai hasil yang sukses atau gagal. Sebagai contoh, jawaban benar suatu pertanyaan pilihan ganda dapat diklasifikasikan sebagai hasil yang sukses, sehingga pilihan jawaban lainnya merupakan jawaban yang salah dan diklasifikasikan sebagai hasil yang gagal. Notasi-notasi yang umumnya digunakan dalam percobaan binomial dan distribusi binomial adalah sebagai berikut.
| Notasi | Keterangan |
| P(S) | Simbol untuk peluang sukses. |
| P(F) | Simbol untuk peluang gagal. |
| p | Peluang sukes. |
| q | Peluang gagal. |
| P(S) = p dan P(F) = 1 – p = q | |
| n | Banyaknya percobaan |
| X | Banyaknya sukses dalam n kali percobaan |
| Perhatikan bahwa 0 ≤ X ≤ n dan X = 0, 1, 2, 3, …, n. | |
Peluang sukses dalam percobaan binomial dapat dihitung dengan menggunakan rumus berikut.
Dalam suatu percobaan binomial, peluang untuk mendapatkan tepat X sukses dalam npercobaan adalah
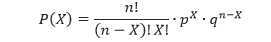
Untuk mengetahui bagaimana ilustrasi dari rumus peluang binomial tersebut bermula, perhatikan Contoh 1 berikut.
Contoh 1: Melempar Koin
Suatu koin dilempar sebanyak tiga kali. Tentukan peluang mendapatkan tepat dua angka.
Pembahasan Permasalahan ini dapat diselesaikan dengan melihat ruang sampelnya. Ruang sampel dari pelemparan satu koin sebanyak tiga kali adalah
S = {AAA, AAG, AGA, GAA, GGA, GAG, AGG, GGG}
Dari ruang sampel, kita dapat melihat bahwa ada tiga cara untuk mendapatkan tepat dua angka, yaitu AAG, AGA, dan GAA. Sehingga peluang kita mendapatkan tepat dua angka adalah 3/8 atau 0,375.
Dengan melihat kembali Contoh 1 dari sudut pandang percobaan binomial, maka contoh tersebut memenuhi keempat kriteria percobaan binomial. - Terdapat tiga kali percobaan.
- Setiap percobaan hanya memiliki dua kemungkinan, yaitu angka (A) atau gambar (G).
- Hasil dari masing-masing percobaan saling bebas (hasil dari suatu pelemparan tidak mempengaruhi hasil pelemparan lainnya).
- Peluang percobaan sukses (angka) adalah ½ di setiap percobaannya.
Dalam kasus ini, n = 3, X = 2, p = ½, dan q = ½. Sehingga dengan mensubstitusi nilai-nilai tersebut ke dalam rumus, kita mendapatkan
Jawaban tersebut sama dengan jawaban kita sebelumnya yang menggunakan ruang sampel.
Contoh 1 tersebut juga dapat digunakan untuk menjelaskan rumus peluang binomial. Pertama, perhatikan bahwa terdapat tiga cara untuk mendapatkan tepat dua angka dan satu gambar dari delapan kemungkinan. Ketiga cara tersebut adalah AAG, AGA, dan GAA. Sehingga, dalam kasus ini banyaknya cara kita mendapatkan dua angka dari pelemparan koin sebanyak tiga kali adalah 3C2, atau 3. Secara umum, banyak cara untuk mendapatkan X sukses dari n percobaan tanpa memperhitungkan urutannya adalah
Ini merupakan bagian pertama rumus binomial. (Beberapa kalkulator dapat digunakan untuk menghitung kombinasi tersebut).
Selanjutnya, masing-masing sukses memiliki peluang ½ dan muncul sebanyak dua kali. Demikian juga masing-masing gagal memiliki peluang ½ dan muncul sekali. Sehingga akan memberikan,pada rumus binomial. Sehingga apabila masing-masing percobaan sukses sukses memiliki peluang p dan muncul X kali serta peluang gagalnya adalah q dan muncul n – X kali, maka dengan menuliskan peluang percobaan sukses kita akan mendapatkan rumus binomial.
Contoh 2: Survei Kunjungan Dokter
Suatu survei menemukan bahwa satu dari lima orang berkata bahwa dia telah mengunjungi dokter dalam sembarang bulan yang ditanyakan. Jika 10 orang dipilih secara acak, berapakah peluang tiga diantaranya sudah mengunjungi dokter bulan lalu?
Pembahasan Pada kasus ini, n = 10, X = 3, p = 1/5, dan q = 4/5. Sehingga,
Jadi peluang tiga orang yang dipilih sudah mengunjungi dokter bulan lalu adalah 0,201.
Menghitung peluang dengan menggunakan rumus binomial bisa menjadi membosankan, sehingga tabel distribusi binomial telah dikembangkan untuk beberapa nilai n dan p.
Contoh 3: Survei Ketakutan untuk Berada di Rumah pada Malam Hari
Suatu lembaga survei melaporkan bahwa 5% orang merasa takut untuk sendirian berada di rumah pada malam hari. Jika 20 orang diambil secara acak, tentukan peluang dengan menggunakan tabel binomial.
- Terdapat 5 orang dalam sampel yang takut sendirian dalam rumah pada malam hari.
- Terdapat paling banyak 3 orang dalam sampel yang takut sendirian dalam rumah pada malam hari.
- Terdapat paling sedikit 3 orang dalam sampel yang takut sendirian dalam rumah pada malam hari.
Pembahasan
1. Pada permasalahan ini, kita mempunyai n = 20, X = 5, dan p = 0,05. Sehingga, dengan melihat tabel binomial kita mendapatkan peluangnya adalah 0,002.

2. Pada soal yang kedua, kita mempunyai n = 20 dan p = 0,05. “Paling banyak 3 orang” berarti 0, atau 1, atau 2, atau 3. Sehingga solusinya adalah
3. Kita memiliki n = 20 dan p = 0,005. “Paling sedikit 3 orang” berarti 3, 4, 5, …, 20. Permasalahan ini dapat diselesaikan dengan menyelesaikan P(0) + P(1) + P(2) kemudian mengurangkannya dari 1.
Jadi, kita peroleh peluangnya adalah 0,076
Ingat bahwa dalam menggunakan distribusi binomial, hasil-hasilnya haruslah saling bebas. Sebagai contoh, dalam pemilihan bola dari kardus yang berisi bola-bola, masing-masing bola haruslah dikembalikan dulu sebelum pengambilan selanjutnya. Jika tidak, maka hasilnya tidaklah saling bebas. Akan tetapi, masalah akan tetap muncul karena terdapat kemungkinan bola yang sama akan terpilih kembali. Permasalahan ini dapat dihilangkan dengan tidak mengembalika bola tersebut dan menggunakan distribusi hipergeometrik untuk menghitung peluangnya. Dan yang perlu diperhatikan, ketika suatu percobaan memiliki populasi yang besar dan sampel yang kecil, dapat ditunjukkan bahwa peluang binomialnya akan mendekati peluang hipergeometriknya.
Rata-rata, Varians, dan Simpangan Baku untuk Distribusi Binomial
Rata-rata, varians, dan simpangan baku variabel yang memiliki distribusi binomial secara berturut-turut dapat ditentukan dengan menggunakan rumus berikut.

Rumus-rumus tersebut secara aljabar ekuivalen dengan rumus-rumus untuk rata-rata, varians, dan simpangan baku variabel distribusi peluang, tetapi karena variabel-variabel tersebut memiliki distribusi binomial, maka variabel-variabel tersebut dapat disederhanakan dengan menggunakan aljabar.
SUMBER REFERENSI :
https://id.wikipedia.org/wiki/Distribusi_binomial
https://yos3prens.wordpress.com/2015/02/01/distribusi-binomial/
http://www.marthamatika.com/2016/09/contoh-soal-dan-pembahasan-distribusi-binomial.html
https://istanamengajar.wordpress.com/2013/11/06/soal-dan-pembahasan-distribusi-probabilitas-binomial-dan-poisson-1-2/
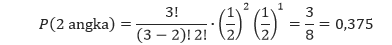
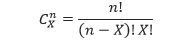
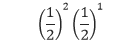
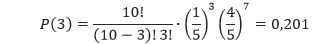
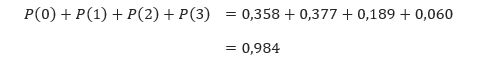
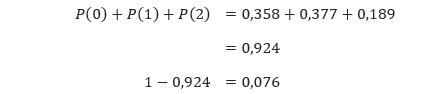
Komentar
Posting Komentar